

| Новые дети | Методы развития детей и взрослых | Первые книги родителей | Продукты | Обратная связь |
|
|
|
Ассоциация одаренных и талантливых детей
|
АРМЭКС. Система
анализа иерархий Примеры
Самое лучшее описание – в рекомендациях по теме: https://studfile.net/preview/3348062/ Указывается, что
расчеты основаны на сведениях и алгоритмах теории матриц Содержание 1. Разработка экспертной системы на основе метода анализа иерархий - Пример содержания 2. Метод анализа иерархий процедура применения3. Лабораторная работа №3 «Разработка динамической модели оценки конкурентной позиции организации на основе метода анализа иерархии»
(пока нет)
1. Разработка экспертной системы на основе Страница курсовой работы на сайте "Курсовик": https://kursovik.com/programming/100810003.html
СОДЕРЖАНИЕ 1. Задание.......................................................3
2. Этапы решения задачи..........................................4
2.1. Описание предметной области.................................4
2.2. Декомпозиция проблемы в иерархию............................5
2.3. Заполнение матриц парных сравнений для уровня 2.............6
2.4. Заполнение матриц парных сравнений для уровня 3.............6
2.5. Оценка векторов приоритетов для уровня 2....................7
2.6. Оценка векторов приоритетов для уровня 3....................9
2.7 Вычисление глобальных приоритетов...........................11
3. Заключение...................................................12
2. Метод анализа иерархий процедура примененияМетод анализа иерархий: процедура примененияСайт:
Общая характеристика метода анализа иерархий Основным достоинством метода анализа иерархий является высокая универсальность – метод может применяться для решения самых разнообразных задач: анализа возможных сценариев развития ситуации, распределения ресурсов, составления рейтинга клиентов, принятия кадровых решений и др. Недостатком метода анализа иерархий является необходимость получения большого объема информации от экспертов. Метод в наибольшей мере подходит для тех случаев, когда основная часть данных основана на предпочтениях лица, принимающего решения, в процессе выбора наилучшего варианта решения из множества существующих альтернатив. В типичной ситуации принятия решения:
Постановка задачи в процессе применения метода анализа иерархий: Пусть имеется множество альтернатив (вариантов решений): В1, В2, … Вk. Каждая из альтернатив оценивается списком критериев: К1, К2, … Кn. Требуется определить наилучшее решение.
Этапы применения метода анализа иерархий: 1. Предварительное ранжирование критериев, в результате которого они располагаются в порядке убывания важности (значимости). 2. Попарное сравнение критериев по важности по девятибалльной шкале с составлением соответствующей матрицы (таблицы) размера (n х n). Система парных сведений приводит к результату, который может быть представлен в виде обратно симметричной матрицы. Элементом матрицы a(i,j) является интенсивность проявления элемента иерархии i относительно элемента иерархии j, оцениваемая по шкале интенсивности от 1 до 9, где оценки имеют следующий смысл:
При этом при проведении попарных сравнений в основном ставятся следующие вопросы при сравнении элементов А и Б:
Затем формируется матрица (схема представлена в Таблице 2). В процессе заполнения матрицы если элемент i важнее элемента j, то клетка (i, j), соответствующая строке i и столбцу j , заполняется целым числом, а клетка (j, i), соответствующая строке j и столбцу i, заполняется обратным числом (дробью). РЕКЛАМА Например, если К1 умеренно превосходит К4, то в клетку (1;4) (на пересечении первой строки и четвертого столбца) ставится число 3, а в клетку (4;1) (четвертая строка первый столбец) – обратная величина, равная 1/3. Если же элемент j более важен, чем элемент i, то целое число ставится в клетку (j, i), а обратная величина – в клетку (i, j). Если считается, что i, j одинаковы, то в обе клетки ставится единица. Заполнение
таблицы (см.примерная схема в табл.2) проводится построчно с наиболее
важного критерия. Сначала проставляют целочисленные оценки, тогда
соответствующие им дробные оценки получаются из них автоматически (как
обратные к целым числам). Чем важнее критерий, тем больше целочисленных
оценок будет в соответствующей ему строке матрицы, и сами оценки имеют
большие значения. Так как каждый критерий равен себе по важности, то главная
диагональ матрицы всегда будет состоять из единиц. Очевидно, что сумма
компонентов равна единице. Каждый компонент НВП представляет собой оценку
важности соответствующего критерия (например, 1-й компонент представляет
собой оценку важности первого критерия). Таблица 1 — Значение показателя случайной согласованности (ПСС)
Оценки в матрице считаются согласованными, если ОС≤10-15%, в противном случае их надо пересматривать. 5. Проводится попарное сравнение вариантов по каждому критерию аналогично тому, как это делалось для критериев, и заполняются соответствующие таблицы (см.ниже – схема представлена в Таблице 3). Для каждой таблицы проводится проверка согласованности локальных приоритетов путем расчета трех характеристик (см.описание 4-го этапа).
РЕКЛАМА 6. Определяется общий критерий (приоритет) для каждого варианта: К(В1) = оценка В1 по первому критерию х 1 й компонент НВП + оценка В1 по второму критерию х 2 й компонент НВП + … + оценка В1 по n му критерию х n й компонент НВП (6) Аналогично подсчитываются К(В2), К(В3) и т.д., при этом в выражении В1 заменяется на В2 , В3 и т.д. соответственно. Заполняется таблица (см.ниже – схема представлена в Таблице 4). 7. Определяется наилучшее решение, для которого значение К максимально. 8. Проверяется достоверность решения:
8.1. расчет обобщенного индекса согласования: ОИС = ИС1 х 1 й компонент НВП + ИС2 х 2 й компонент НВП + … + ИСnх n й компонент НВП (7) 8.2. расчет обобщенного отношения согласованности: ООС = ОИС/ ОПСС (8) где ОПСС определяется по таблице 1 на уровне ПСС (показателя случайной согласованности) для матриц сравнения вариантов по критериям. Решение считается достоверным, если ООС≤10-15%, в противном случае нужно корректировать матрицы сравнения вариантов по критериям. Таблица 2 — Форма таблицы сравнения критериев
Таблица 3 — Форма таблицы сравнения вариантов по критериям (заполняется по каждому j-му критерию сравнения Kj j=1,n) Матрица попарного сравненияМатрица попарного сравнения – инструмент количественного анализа при принятии решений, который позволяет команде значительно упростить нередко такой запутанный процесс определения приоритетов.
Применимость инструментаКаждому члену команды необходимо выбрать один из предлагаемых попарно вариантов, включающих несколько различных задач, над которыми предлагается работать, или несколько решений, которые предлагается проверить. Данный инструмент легче всего использовать в условиях, когда количество имеющихся вариантов относительно невелико, так как если принять количество вариантов за N, то число сравнений равно = N(N – 1), например:
Пошаговая инструкция для оценки метода попарного сравнения1).
Распечатайте матрицу или начертите ее на флипчарте или доске. В левой части
матрицы перечислите все имеющиеся варианты (возможности «прорывов» и т.д.).
Похожее: Фмба узнать результаты анализов
Например, проводя опрос участников относительно варианта А, начинайте с пары «А или В», задавая участникам вопрос: «Если нужно выбрать между А и В, то кто из вас выбрал бы А?» Зафиксируйте количество голосов, полученных за «А», и переходите к паре «А или С», задавая вопрос: «Если нужно выбрать между А и С, то кто из вас выбрал бы С?» Когда закончите опрос по всем парам, в которых есть вариант А, проделайте то же самое для вариантов В, С, D и E. Примечание: Не во всех парах из перечисленных в верхней части матрицы будет содержатся тот вариант, за который голосуют участники, в таких случаях оставляйте соответствующую клетку матрицы чистой или зачеркните ее.
6).
Проверьте результаты голосования, суммируйте голоса, поставленные под каждой
парой. Итоговые значения должны быть равны числу членов команд (-ы),
принимающих участие в голосовании. Примечание
Используемый материал: 1.
Томас Джексон «Хосин канри: как заставить стратегию работать». Пер. с англ.
– М.: Институт комплексных стратегических исследований, 2008. – 248с. Матрица решений, матричный анализ, метод ПьюПредставьте себе, что ваш начальник назначил вас руководить выбором новых внештатных поставщиков продуктов IT. Вы уже нашли несколько разных поставщиков, и теперь вам нужно выбрать с кем из них заключить договор. Можно было бы использовать критерий минимальных затрат. Но вы же не хотите основывать свое решение только на стоимости – необходимо принимать во внимание и такие факторы, как длительность контракта, применяемые технологии и качество обслуживания. И как же вы можете убедиться, что вы приняли лучшее решение, принимая во внимание все эти различные факторы? Метод матрицы решений представляет собой полезный инструмент для принятия подобных решений. Его сила в наибольшей степени проявляется тогда, когда вам предстоит сделать выбор из набора подходящих альтернатив и при этом учесть несколько различных факторов. Научившись применять метод матрицы решений вы можете уверенно и рационально принимать решения. Как использовать матричный анализМетод матрицы решений работает так: вы составляете таблицу, где заголовками строк будет список вариантов из которых нужно сделать выбор, а заголовками столбцов будут факторы, которые нужно учесть. Далее вы оцениваете каждую комбинацию вариант/фактор, используя для этой оценки весовой коэффициент.. Затем полученные оценки суммируются для каждого варианта решения и вы получаете общую оценку. Может звучать несколько сложно, но данный метод довольно все же прост в использовании. Рассмотрим пошаговое руководство с примером. Шаг 1Запишите все ваши варианты решений в первой колонке таблицы в качестве названий строк таблицы, и перечислите факторы, которые нужно рассмотреть, в качестве названий столбцов. Например, если вы покупаете новый ноутбук, факторами для рассмотрения могут быть стоимость, размеры и емкость жесткого диска, вес, размер экрана и т.п. Шаг 2Теперь заполняйте ячейки вашей таблицы, оценивая каждый вариант выбора решения для каждого фактора. Оценка варианта может находиться в пределах от 0 (плохо) до 5 (отлично). Заметим, что вы не обязаны проставлять разные оценки для каждого варианта – если ни один из них не подходит для конкретного фактора в вашем решении, то все они могут получить оценку 0. Шаг 3Следующим шагом является определение относительной важности факторов в принятии решения. Обозначьте ее числами, скажем от 0 до 5, где 0 означает, что данный фактор совершенно неважен для окончательного решения, а 5 означает, что он весьма важен. (Вполне допустимо иметь факторы с одинаковой важностью.) Расчет матриц сравнения и приоритетовДля проведения субъективных парных сравнений разработана шкала, приведенная в таблице 5.3.1. Данной шкалой я воспользуюсь дальше для заполнения матрицы критериев и матрицы альтернатив. Таблица 5.3.1 Шкала относительной важности
Используя таблицу 5.2, заполняем матрицу попарных сравнений для уровня 2. Для этого необходимо заполнить строки матрицы соответствующими значениями важности, при сравнении критериев на втором уровне. Для каждого последующего уровня иерархии строятся дополнительные матрицы. Для сравнения радиомодема вопросы, которые следует задавать при сравнении двух критериев на втором уровне, будут такого рода, который из двух сравниваемых критериев считается более важным (например, частота по отношению к чувствительности) и насколько он более важен именно по отношению к цели «радиомодем»? Аналогично на третьем уровне следует спросить, какой из сравниваемых альтернатив предпочтительнее и насколько он более желателен по отношению к определенному критерию (например, критерию 1) второго уровня, по которому производится сравнение? По соглашению сравнивается относительная важность левых элементов матрицы с элементами наверху. Поэтому если элемент слева важнее, чем элемент наверху, то в клетку заносится положительное целое число от 1 до 9, в противном случае — обратное число (дробь).
Относительная важность любого элемента, сравниваемого с самим собой, равна 1; поэтому диагональ матрицы (элементы от левого верхнего угла до нижнего правого) содержит только единицы. Наконец, обратными величинами заполняют симметричные клетки, т. е. если элемент А воспринимается как «слегка более важный» (3 на шкале), относительно элемента Б, то считаем, что элемент Б «слегка менее важен» (1/3 на шкале) относительно элемента А. Таблица 5.3.2 Матрица попарных сравнении уровня 2
По данным вычислений, самым значимым критерием, оказался критерий 5 (помехозащищенность). Вектор приоритетов вычисляется следующим образом: элементы каждой строки перемножаются, и затем извлекается корень n-й степени, где n- число элементов (в данном случае n=5). Полученный столбец нормализуется делением каждого числа на сумму всех чисел.
Оценить
степень согласованности, позволяет индекс согласованности (ИС). Он
определяется следующим образом: суммируется каждый столбец суждений, затем
сумма первого столбца умножается на величину вектора приоритетов матрицы и
т.д. Полученные числа суммируются, получая наибольшее собственное значение
матрицы суждений ИС= где n —
число элементов, а Отношение согласованности (ОС) можно найти по следующей формуле: ОС= В результате вычислений программы «PRIMEN», получились следующие значения:
Теперь заполняем матрицы альтернатив (матрицы попарных сравнений уровня 3). Эти матрицы заполняются по аналогичному принципу, что и матрица попарных сравнений уровня 2. Только теперь мы сравниваем альтернативы (радиомодемы) по основным пяти критериям обозначенными выше.
Похожее: 187183 Полисемия как результат концептуальной интеграции
Таблица 5.3.3 Сравнение радиомодемов по критерию 1 (рабочая частота)
В результате сравнения радиомодемов, по критерию 1 (по рабочей частоте), получилось, что по локальным приоритетам «Мета» и «ГАММА» оказались больше, чем у «Риф Файндер — 801», следовательно, по данному критерию они лучше. Таблица 5.3.3 Сравнение радиомодемов по критерию 2 (мощность передатчика)
При сравнении радиомодемов, по критерию 2, мы выяснили, что локальные приоритеты модемов одинаковые. Т.к. мощность всех трех передатчиков одинакова. Таблица 5.3.4 Сравнение радиомодемов по критерию 3 (скорость передачи)
В результате сравнения радиомодемов, по критерию 3, локальный приоритет радиомодемов «Мета» и «ГАММА» больше чем у «Риф Файндер — 801», следовательно, по данному критерию они выигрывают. Таблица 5.3.5 Сравнение радиомодемов по критерию 4(чувствительность)
В результате сравнения радиомодемов, по критерию 4, локальный приоритет радиомодемов «Мета» и «Риф Файндер — 801» больше чем у «ГАММА», следовательно, по данному критерию они выигрывают. Таблица 5.3.6 Сравнение радиомодемов по критерию 5 (Помехозащищенность)
В результате сравнения по данному критерию, локальный приоритет больше у радиомодема «МЕТА». Результирующая матрица выглядит следующим образом: Таблица 5.3.7 Матрица глобальных приоритетов
Согласованность всей иерархии можно найти следующим образом; необходимо перемножить каждый индекс согласованности на приоритет соответствующего критерия и просуммировать полученные числа. Результат делится на выражение такого же типа, только со случайным индексом согласованности: СИ= Следовательно, результаты анализа следует считать верными, так как СИ<10…20%. По результатам анализа установлено, что радиомодем «МЕТА», является конкурентоспособным. Он преимущественно выигрывает по техническим характеристикам у своих прямых конкурентов: «ГАММА» и «Риф Файндер — 801». Все вышеприведенные расчеты произведены с помощью программы “PRIMEN”, разработанной в СибГАТИ. Заключение Задача данной курсовой работы состояла в определении конкурентоспособности радиомодема «МЕТА» по сравнению с двумя заданными. Мной были определены затраты как на отдельные аспекты разработки радиомодема, так и конечная (рыночная) стоимость нашего модема. Наш радиомодем отличается немалой стоимостью и неплохими характеристиками по сравнению с конкурентами. Методом иерархий установлено, что радиомодем МЕТА все же выигрывает по своим параметрам у прямых конкурентов по следующим приоритетам. По локальным приоритетам: ) по критерию 1(частота) преимущество у радиомодемов «МЕТА» и «ГАММА», так как у данных модемов частота переменная (перестраиваемая); ) мощность передатчика у радиомодемов одинаковая, следовательно, приоритет у всех трех одинаковый, так как мощность равна 10мВт; ) скорость передачи у радиомодемов «МЕТА» и «ГАММА» одинаковая, следовательно, они имеют преимущество по отношению к модему «Риф Файндер — 801»; ) чувствительность у радиомодемов «МЕТА» и «Риф Файндер — 801» одинаковая, следовательно, они имеют преимущество пред модемом «ГАММА»; ) помехозащищенность у радиомодема «МЕТА» выше, чем у «ГАММА» и «Риф Файндер — 801». Что же касается глобальных приоритетов, то по пяти критериям сравнения радиомодема «МЕТА» значительно превосходит конкурентов, с которыми производилось сравнение. Библиография 1. Н.С. Кичайкина, Е.И Чернышевская. Оценка стоимости объектов интеллектуальной собственности. Методические рекомендации/ СибГУТИ: Новосибирск, 2002. — 40с. Матричные методы стратегического анализа. Классификация и внедрениеВ стратегическом планировании и маркетинге применяется достаточно много матриц той или иной направленности. Существует необходимость систематизации этих матриц, а также поэтапного внедрения матричного подхода на всех этапах стратегического анализа и планирования. Уровни стратегического планирования при матричном измерении. В стратегическом планировании можно выделить уровень корпорации, бизнес-уровень, функциональный уровень. Матрицы стратегического планирования на уровне корпорации анализируют входящие в корпорацию бизнесы, т.е. помогают осуществлять портфельный анализ, а также анализ ситуации в корпорации в целом. Бизнес-уровень включает матрицы, которые имеют отношение к данной бизнес-единице. Матрицы и относятся чаще всего к одному товару, анализируют свойства этого товара, ситуацию на рынке данного товара и т.д. Матрицы функционального уровня исследуют факторы, влияющие на функциональные сферы предприятия, из которых наиболее важными являются маркетинг, управление персоналом. Классификация матриц стратегического анализа и планирования.Существующие матрицы стратегического анализа и планирования исследуют различные аспекты данного процесса. Классификация матриц необходима для выявления закономерностей и особенностей применения матричного метода в стратегическом анализе и планировании. Матрицы по существующим признакам можно классифицировать следующим образом:
Классификация по количеству исследуемых ячеек.
Чем больше ячеек содержит матрица, тем она сложнее и более информативна. В этом случае возможно деление матриц на четыре группы. К первой группе относятся матрицы, состоящие из четырех ячеек. Во второй группе находятся матрицы, состоящие из девяти ячеек, в третьей — из шестнадцати, в четвертой — более шестнадцати ячеек. Классификация по объекту изучения делит матрицы на группы в зависимости от изучаемого объекта. В матрице «Осведомленность – отношение» объектом изучения является персонал, так же как и в матрице «Влияние оплаты на взаимоотношения в группе». Другим объектом исследования выступает портфель компании. В этой группе примерами могут служить матрицы Shell/DPM, BCG. Внедрение матричного инструментария в анализ и планирование деятельности предприятия.На первом этапе предлагается произвести первичный анализ деятельности предприятия. Для этой цели подобраны три матрицы. Матрица SWOT широко описана в литературе. Матрица MCC предполагает анализ соответствия миссии предприятия и его основных возможностей. Матрица вектора экономического развития предприятия представляет собой таблицу, в которой представлены числовые данные основных показателей предприятия. Из этой матрицы можно почерпнуть информацию для других матриц, а также на основе этих данных сделать различные выводы уже на данном этапе. Вторым этапом применения матричных методов является анализ рынка и отрасли. Здесь анализируются рынки, на которых функционирует предприятие, а также отрасль в целом. Основными в подгруппе «Рынок» являются матрица BCG, исследующая зависимость темпов роста и доли рынка, и матрица GE, анализирующая сравнительную привлекательность рынка и конкурентоспособность в отрасли и имеющая две разновидности: вариант Дэйа и вариант Мониенсона. Подгруппа «Отрасль» содержит матрицы, исследующие отраслевое окружение, закономерности развития отрасли. Основной в данной подгруппе является матрица Shell/DPM, исследующая зависимость отраслевой привлекательности и конкурентоспособности. Следующие этапы стратегического планирования – анализ дифференциации и анализ качества. Дифференциация и качество выступают в данном случае как составляющие, с помощью которых возможно получение требуемого результата. В группе «Дифференциация» находятся три матрицы. Матрица «Улучшение конкурентной позиции» позволяет наглядно выявить закономерности и зависимости дифференциации от охвата рынка. Матрица «Дифференциация – относительная эффективность затрат» выявляет зависимость относительной эффективности затрат на данном рынке от дифференциации. Матрица «Производительность – инновации/дифференциации» показывает зависимость между производительностью данной бизнес-единицы и внедрением инноваций. Объект исследования группы «Анализ качества» – выявление факторов и закономерностей, влияющих на такой аспект, как качество производимой продукции. Группа может включать две матрицы. Матрица «Стратегии установления цен» позиционирует продукты в зависимости от качества и цены. Матрица «Качество – ресурсоемкость» определяет соотношение качества произведенного продукта и ресурсов, на него потраченных. Группы «Анализ управления» и «Анализ маркетинговой стратегии» не входят в процесс пошагового внедрения матричного метода в стратегическое планирование. Эти группы являются обособленными. Матрицы, из которых состоят данные группы, могут применяться на всех стадиях стратегического планирования и затрагивают вопросы функционального планирования. Группа «Анализ управления» состоит из двух подгрупп. Первая подгруппа — «Руководство» — рассматривает руководство компании в целом, процессы, влияющие на руководство, менеджмент компании. Подгруппа «Персонал» рассматривает процессы, протекающие между сослуживцами, влияние различных факторов на работоспособность персонала. В предложенной схеме стратегического анализа и планирования в каждой группе матрицы взаимодействуют друг с другом, но нельзя опираться на результат или вывод только одной матрицы – необходимо учитывать выводы, получаемые из каждой матрицы в группе. После проведения анализа в первой группе проводится анализ в следующей. Анализ в группах «Управление» и «Маркетинговая стратегия» осуществляется на всех этапах анализа в стратегическом планировании. Характеристика отдельных матрицSWOT-анализ – это один из самых распространенных видов анализа в стратегическом управлении на сегодняшний день. SWOT: Strengths (Cилы); Weaknesses (Слабости); Opportunities (Возможности); Threats (Угрозы). SWOT-анализ позволяет выявить, структурировать сильные и слабые стороны компании, а также потенциальные возможности и угрозы. Достигается это за счет сравнения внутренних сил и слабостей своей компании с возможностями, которые дает им рынок. Исходя из качества соответствия, делается вывод о том, в каком направлении организация должна развивать свой бизнес, и в конечном итоге определяется распределение ресурсов по сегментам. Цель SWOT-анализа – сформулировать основные направления развития предприятия через систематизацию имеющейся информации о сильных и слабых сторонах фирмы, а также о потенциальных возможностях и угрозах. Самое привлекательное, в этом методе то, что информационное поле формируется непосредственно самими руководителями, а также наиболее компетентными сотрудниками компании на основании обобщения и согласования собственного опыта и видения ситуации. Общий вид матрицы первичного SWOT-анализа приведен на Рис.1.
Рис.1. Матрица первичного стратегического SWOT — анализа. На основании последовательного рассмотрения факторов, принимаются решения по корректировке целей и стратегий предприятия (корпоративных, продуктовых, ресурсных, функциональных, управленческих), которые, в свою очередь, определяют ключевые моменты организации деятельности. Анализ бизнес-портфеля компании должен помочь менеджерам оценить поле деятельности компании. Компания должна стремиться вкладывать средства в более прибыльные области своей деятельности и сокращать убыточные. Первым шагом руководящего звена при анализе бизнес-портфеля является выявление ключевых направлений деятельности, определяющих миссию компании. Их можно назвать стратегическими элементами бизнеса – СЭБ. На следующем этапе анализа бизнес-портфеля руководство должно оценить привлекательность различных СЭБ и решить, какой поддержки заслуживает каждое из них. В некоторых компаниях это происходит неформально в процессе работы. Руководство изучает совокупность направлений деятельности и товаров компании и, руководствуясь здравым смыслом, решает, сколько каждый СЭБ должен приносить и получать. Другие компании используют формальные методы для планирования портфеля. Формальные методы можно назвать более точными и основательными. Среди наиболее известных и удачных методов анализа бизнес-портфеля с помощью формальных методов можно назвать следующие: компании Boston Consulting Group (BCG);
Метод BCG основан на принципе анализа матрицы рост/доля рынка. Этот метод планирования портфеля, который оценивает СЭБ компании с точки зрения темпов роста их рынка и относительной доли этих элементов на рынке. СЭБ делятся на «звезд», «дойных коров», «темных лошадок» и «собак» (см. рис. 2). Рис.2. Матрица BCG. Вертикальная ось на рис.2, темпы роста рынка, определяет меру привлекательности рынка. Горизонтальная ось, относительная доля рынка, определяет прочность положения компании на рынке. При делении матрицы рост/доля рынка на секторы можно выделить четыре типа СЭБ. «Звезды». Быстро развивающиеся направления деятельности, товары, имеющие большую долю рынка. Они требуют обычно мощного инвестирования для поддержания своего роста. Со временем их рост замедляется, и они превращаются в «дойных коров». «Дойные коровы». Направления деятельности или товары с низкими темпами роста и большой долей рынка. Этим устойчивым преуспевающим СЭБ для удержания их доли рынка требуется меньше инвестиций. При этом они приносят высокий доход, который компания использует для оплаты своих счетов и для поддержания других СЭБ, требующих инвестирования. «Темные лошадки». Элементы бизнеса, имеющие небольшую долю быстрорастущих рынков. Они требуют большого количества средств даже для поддержания своей доли рынка, не говоря уже об ее увеличении. Руководству следует тщательно продумать, каких «темных лошадок» стоит превратить в «звезды», а какие поэтапно ликвидировать. «Собаки». Направления деятельности и товары с низкой скоростью роста и небольшой долей рынка. Они могут приносить достаточный доход для поддержания самих себя, но не обещают стать более серьезными источниками дохода. Каждый СЭБ выносится на данную матрицу пропорционально ее доли в валовом доходе компании. После классификации СЭБ компания должна определить роль каждого элемента в будущем. В отношении каждого СЭБ можно применить одну из четырех стратегий. Компания может увеличить инвестиции в какой-либо элемент бизнеса, чтобы отвоевать для него долю рынка. Либо она может инвестировать ровно столько, сколько нужно для сохранения доли СЭБ на текущем уровне. Она может выкачивать ресурсы из СЭБ, изымая его краткосрочные денежные ресурсы в течение определенного промежутка времени, не считаясь с отдаленными последствиями. Наконец, она может изъять капиталовложения из СЭБ, продав его или приступив к поэтапной ликвидации, и использовать ресурсы в другом месте. С течением времени СЭБ меняет свое положение в матрице рост/доля рынка. У каждого СЭБ свой жизненный цикл. Многие СЭБ начинают как «темные лошадки» и при благоприятно складывающихся обстоятельствах переходят в категорию «звезд». Позже, по мере замедления роста рынка, они становятся «дойными коровами» и, наконец, на закате своего жизненного цикла угасают или превращаются в «собак». Компании необходимо непрерывно вводить новые товары и виды деятельности, чтобы часть из них становилась «звездами», а затем и «дойными коровами», помогающими финансировать другие СЭБ. Матричные методы играют очень важную роль в стратегическом анализе, планировании и маркетинге. Матричный метод очень удобен – именно этим объясняется его распространенность. Однако использование только матричных методов не является достаточным, так как матрицы позволяют исследовать стратегическое планирование и маркетинг с отдельных сторон, и не показывают полной картины, но в соединении с остальными методами матричный подход дает возможность наглядно увидеть закономерности в процессах, происходящих на предприятии, и сделать правильные выводы. Таблица 1. Матричный инструментарий в анализе и планировании деятельности организации
3. Лабораторная работа №3 «Разработка динамической
|
| Важность | Определение |
| 1 | Равная важность |
| 2 | Промежуточное решение между соседними |
| 3 | Умеренное превосходство |
| 4 | Промежуточное решение между соседними |
| 5 | Существенное превосходство |
| 6 | Промежуточное решение между соседними |
| 7 | Значительное превосходство |
| 8 | Промежуточное решение между соседними |
| 9 | Очень сильное превосходство |
Используя таблицу 5.2, заполняем матрицу попарных сравнений для уровня 2. Для этого необходимо заполнить строки матрицы соответствующими значениями важности, при сравнении критериев на втором уровне.
Для каждого последующего уровня иерархии строятся дополнительные матрицы. Для сравнения радиомодема вопросы, которые следует задавать при сравнении двух критериев на втором уровне, будут такого рода, который из двух сравниваемых критериев считается более важным (например, частота по отношению к чувствительности) и насколько он более важен именно по отношению к цели «радиомодем»? Аналогично на третьем уровне следует спросить, какой из сравниваемых альтернатив предпочтительнее и насколько он более желателен по отношению к определенному критерию (например, критерию 1) второго уровня, по которому производится сравнение?
По соглашению сравнивается относительная важность левых элементов матрицы с элементами наверху. Поэтому если элемент слева важнее, чем элемент наверху, то в клетку заносится положительное целое число от 1 до 9, в противном случае — обратное число (дробь).
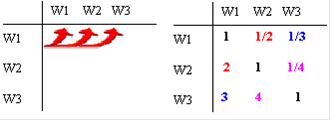
Относительная важность любого элемента, сравниваемого с самим собой, равна 1; поэтому диагональ матрицы (элементы от левого верхнего угла до нижнего правого) содержит только единицы. Наконец, обратными величинами заполняют симметричные клетки, т. е. если элемент А воспринимается как «слегка более важный» (3 на шкале), относительно элемента Б, то считаем, что элемент Б «слегка менее важен» (1/3 на шкале) относительно элемента А.
Таблица 5.3.2 Матрица попарных сравнении уровня 2
| Критерий № | 1 | 2 | 3 | 4 | 5 | Вектор приоритетов |
| 1 | 1 | 1/2 | 1/2 | 1/3 | 1/5 | 0,0735 |
| 2 | 2 | 1 | 1/2 | 1/3 | 1/2 | 0,1164 |
| 3 | 2 | 2 | 1 | 1/3 | 1/3 | 0,1417 |
| 4 | 3 | 3 | 3 | 1 | 1/3 | 0,2586 |
| 5 | 5 | 2 | 3 | 3 | 1 | 0,4098 |
По данным вычислений, самым значимым критерием, оказался критерий 5 (помехозащищенность).
Вектор приоритетов вычисляется следующим образом: элементы каждой строки перемножаются, и затем извлекается корень n-й степени, где n- число элементов (в данном случае n=5). Полученный столбец нормализуется делением каждого числа на сумму всех чисел.

Оценить степень согласованности, позволяет индекс согласованности (ИС). Он
определяется следующим образом: суммируется каждый столбец суждений, затем
сумма первого столбца умножается на величину вектора приоритетов матрицы и
т.д. Полученные числа суммируются, получая наибольшее собственное значение
матрицы суждений 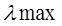 .
Тогда:
.
Тогда:
ИС= 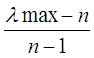 ,
,
где n — число элементов, а 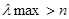
Отношение согласованности (ОС) можно найти по следующей формуле:
ОС= 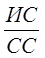 ,
,
В результате вычислений программы «PRIMEN», получились следующие значения:
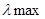 =5,341
=5,341
Теперь заполняем матрицы альтернатив (матрицы попарных сравнений уровня 3).
Эти матрицы заполняются по аналогичному принципу, что и матрица попарных сравнений уровня 2. Только теперь мы сравниваем альтернативы (радиомодемы) по основным пяти критериям обозначенными выше.
Таблица 5.3.3 Сравнение радиомодемов по критерию 1 (рабочая частота)
| Критерий 1 | Альтернатива 1 | Альтернатива 2 | Альтернатива 3 | Вектор приоритетов |
| Альтернатива 1 | 1 | 7 | 2 | 0,5736 |
| Альтернатива 2 | 1/7 | 1 | 1/7 | 0,0650 |
| Альтернатива 3 | 1/2 | 7 | 1 | 0,3614 |
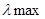 =3,0536;
=3,0536;
В результате сравнения радиомодемов, по критерию 1 (по рабочей частоте), получилось, что по локальным приоритетам «Мета» и «ГАММА» оказались больше, чем у «Риф Файндер — 801», следовательно, по данному критерию они лучше.
Таблица 5.3.3 Сравнение радиомодемов по критерию 2 (мощность передатчика)
| Критерий 2 | Альтернатива 1 | Альтернатива 2 | Альтернатива 3 | Вектор приоритетов |
| Альтернатива 1 | 1 | 1 | 1 | 0,3333 |
| Альтернатива 2 | 1 | 1 | 1 | 0,3333 |
| Альтернатива 3 | 1 | 1 | 1 | 0,3333 |
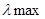 =3;
=3;
При сравнении радиомодемов, по критерию 2, мы выяснили, что локальные приоритеты модемов одинаковые. Т.к. мощность всех трех передатчиков одинакова.
Таблица 5.3.4 Сравнение радиомодемов по критерию 3 (скорость передачи)
| Критерий 3 | Альтернатива 1 | Альтернатива 2 | Альтернатива 3 | Вектор приоритетов |
| Альтернатива 1 | 1 | 7 | 2 | 0,5736 |
| Альтернатива 2 | 1/7 | 1 | 1/7 | 0,0650 |
| Альтернатива 3 | 1/2 | 7 | 1 | 0,3614 |
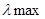 =3,0536;
=3,0536;
В результате сравнения радиомодемов, по критерию 3, локальный приоритет радиомодемов «Мета» и «ГАММА» больше чем у «Риф Файндер — 801», следовательно, по данному критерию они выигрывают.
Таблица 5.3.5 Сравнение радиомодемов по критерию 4(чувствительность)
| Критерий 4 | Альтернатива 1 | Альтернатива 2 | Альтернатива 3 | Вектор приоритетов |
| Альтернатива 1 | 1 | 1/2 | 7 | 0,3614 |
| Альтернатива 2 | 2 | 1 | 7 | 0,5736 |
| Альтернатива 3 | 1/7 | 1/7 | 1 | 0,0650 |
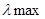 =3,0536;
=3,0536;
В результате сравнения радиомодемов, по критерию 4, локальный приоритет радиомодемов «Мета» и «Риф Файндер — 801» больше чем у «ГАММА», следовательно, по данному критерию они выигрывают.
Таблица 5.3.6 Сравнение радиомодемов по критерию 5 (Помехозащищенность)
| Критерий 5 | Альтернатива 1 | Альтернатива 2 | Альтернатива 3 | Вектор приоритетов |
| Альтернатива 1 | 1 | 7 | 7 | 0,7732 |
| Альтернатива 2 | 1/7 | 1 | 1/2 | 0,0877 |
| Альтернатива 3 | 1/7 | 2 | 1 | 0,1392 |
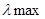 =3,0536;
=3,0536;
В результате сравнения по данному критерию, локальный приоритет больше у радиомодема «МЕТА».
Результирующая матрица выглядит следующим образом:
Таблица 5.3.7 Матрица глобальных приоритетов
| Критерий 1 (0,073) | Критерий 2 (0,116) | Критерий 3 (0,142) | Критерий 4 (0,259) | Критерий 5 (0,410) | Глобальные приоритеты | |
| Альтернатива 1 | 0,5736 | 0,3333 | 0,5736 | 0,3614 | 0,7732 | 0,5725 |
| Альтернатива 2 | 0,0650 | 0,3333 | 0,0650 | 0,5736 | 0,0877 | 0,2371 |
| Альтернатива 3 | 0,3614 | 0,3333 | 0,3614 | 0,0650 | 0,1392 | 0,1904 |
Согласованность всей иерархии можно найти следующим образом; необходимо перемножить каждый индекс согласованности на приоритет соответствующего критерия и просуммировать полученные числа. Результат делится на выражение такого же типа, только со случайным индексом согласованности:
СИ= 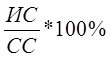 ,
,
Следовательно, результаты анализа следует считать верными, так как СИ<10…20%.
По результатам анализа установлено, что радиомодем «МЕТА», является конкурентоспособным. Он преимущественно выигрывает по техническим характеристикам у своих прямых конкурентов: «ГАММА» и «Риф Файндер — 801».
Все вышеприведенные расчеты произведены с помощью программы “PRIMEN”, разработанной в СибГАТИ.
Заключение
Задача данной курсовой работы состояла в определении конкурентоспособности радиомодема «МЕТА» по сравнению с двумя заданными. Мной были определены затраты как на отдельные аспекты разработки радиомодема, так и конечная (рыночная) стоимость нашего модема. Наш радиомодем отличается немалой стоимостью и неплохими характеристиками по сравнению с конкурентами.
Методом иерархий установлено, что радиомодем МЕТА все же выигрывает по своим параметрам у прямых конкурентов по следующим приоритетам.
По локальным приоритетам:
) по критерию 1(частота) преимущество у радиомодемов «МЕТА» и «ГАММА», так как у данных модемов частота переменная (перестраиваемая);
) мощность передатчика у радиомодемов одинаковая, следовательно, приоритет у всех трех одинаковый, так как мощность равна 10мВт;
) скорость передачи у радиомодемов «МЕТА» и «ГАММА» одинаковая, следовательно, они имеют преимущество по отношению к модему «Риф Файндер — 801»;
) чувствительность у радиомодемов «МЕТА» и «Риф Файндер — 801» одинаковая, следовательно, они имеют преимущество пред модемом «ГАММА»;
) помехозащищенность у радиомодема «МЕТА» выше, чем у «ГАММА» и «Риф Файндер — 801».
Что же касается глобальных приоритетов, то по пяти критериям сравнения радиомодема «МЕТА» значительно превосходит конкурентов, с которыми производилось сравнение.
Библиография
1. Н.С. Кичайкина, Е.И Чернышевская. Оценка стоимости объектов интеллектуальной собственности. Методические рекомендации/ СибГУТИ: Новосибирск, 2002. — 40с.
В стратегическом планировании и маркетинге применяется достаточно много матриц той или иной направленности. Существует необходимость систематизации этих матриц, а также поэтапного внедрения матричного подхода на всех этапах стратегического анализа и планирования.
Уровни стратегического планирования при матричном измерении. В стратегическом планировании можно выделить уровень корпорации, бизнес-уровень, функциональный уровень.
Матрицы стратегического планирования на уровне корпорации анализируют входящие в корпорацию бизнесы, т.е. помогают осуществлять портфельный анализ, а также анализ ситуации в корпорации в целом.
Бизнес-уровень включает матрицы, которые имеют отношение к данной бизнес-единице. Матрицы и относятся чаще всего к одному товару, анализируют свойства этого товара, ситуацию на рынке данного товара и т.д.
Матрицы функционального уровня исследуют факторы, влияющие на функциональные сферы предприятия, из которых наиболее важными являются маркетинг, управление персоналом.
Существующие матрицы стратегического анализа и планирования исследуют различные аспекты данного процесса. Классификация матриц необходима для выявления закономерностей и особенностей применения матричного метода в стратегическом анализе и планировании.
Матрицы по существующим признакам можно классифицировать следующим образом:
Чем больше ячеек содержит матрица, тем она сложнее и более информативна. В этом случае возможно деление матриц на четыре группы. К первой группе относятся матрицы, состоящие из четырех ячеек. Во второй группе находятся матрицы, состоящие из девяти ячеек, в третьей — из шестнадцати, в четвертой — более шестнадцати ячеек.
Классификация по объекту изучения делит матрицы на группы в зависимости от изучаемого объекта. В матрице «Осведомленность – отношение» объектом изучения является персонал, так же как и в матрице «Влияние оплаты на взаимоотношения в группе». Другим объектом исследования выступает портфель компании. В этой группе примерами могут служить матрицы Shell/DPM, BCG.
На первом этапе предлагается произвести первичный анализ деятельности предприятия. Для этой цели подобраны три матрицы. Матрица SWOT широко описана в литературе. Матрица MCC предполагает анализ соответствия миссии предприятия и его основных возможностей. Матрица вектора экономического развития предприятия представляет собой таблицу, в которой представлены числовые данные основных показателей предприятия. Из этой матрицы можно почерпнуть информацию для других матриц, а также на основе этих данных сделать различные выводы уже на данном этапе.
Вторым этапом применения матричных методов является анализ рынка и отрасли. Здесь анализируются рынки, на которых функционирует предприятие, а также отрасль в целом. Основными в подгруппе «Рынок» являются матрица BCG, исследующая зависимость темпов роста и доли рынка, и матрица GE, анализирующая сравнительную привлекательность рынка и конкурентоспособность в отрасли и имеющая две разновидности: вариант Дэйа и вариант Мониенсона. Подгруппа «Отрасль» содержит матрицы, исследующие отраслевое окружение, закономерности развития отрасли. Основной в данной подгруппе является матрица Shell/DPM, исследующая зависимость отраслевой привлекательности и конкурентоспособности.
Следующие этапы стратегического планирования – анализ дифференциации и анализ качества. Дифференциация и качество выступают в данном случае как составляющие, с помощью которых возможно получение требуемого результата. В группе «Дифференциация» находятся три матрицы. Матрица «Улучшение конкурентной позиции» позволяет наглядно выявить закономерности и зависимости дифференциации от охвата рынка. Матрица «Дифференциация – относительная эффективность затрат» выявляет зависимость относительной эффективности затрат на данном рынке от дифференциации. Матрица «Производительность – инновации/дифференциации» показывает зависимость между производительностью данной бизнес-единицы и внедрением инноваций.
Объект исследования группы «Анализ качества» – выявление факторов и закономерностей, влияющих на такой аспект, как качество производимой продукции. Группа может включать две матрицы. Матрица «Стратегии установления цен» позиционирует продукты в зависимости от качества и цены. Матрица «Качество – ресурсоемкость» определяет соотношение качества произведенного продукта и ресурсов, на него потраченных.
Группы «Анализ управления» и «Анализ маркетинговой стратегии» не входят в процесс пошагового внедрения матричного метода в стратегическое планирование. Эти группы являются обособленными. Матрицы, из которых состоят данные группы, могут применяться на всех стадиях стратегического планирования и затрагивают вопросы функционального планирования. Группа «Анализ управления» состоит из двух подгрупп. Первая подгруппа — «Руководство» — рассматривает руководство компании в целом, процессы, влияющие на руководство, менеджмент компании. Подгруппа «Персонал» рассматривает процессы, протекающие между сослуживцами, влияние различных факторов на работоспособность персонала.
В предложенной схеме стратегического анализа и планирования в каждой группе матрицы взаимодействуют друг с другом, но нельзя опираться на результат или вывод только одной матрицы – необходимо учитывать выводы, получаемые из каждой матрицы в группе. После проведения анализа в первой группе проводится анализ в следующей. Анализ в группах «Управление» и «Маркетинговая стратегия» осуществляется на всех этапах анализа в стратегическом планировании.
SWOT-анализ – это один из самых распространенных видов анализа в стратегическом управлении на сегодняшний день. SWOT: Strengths (Cилы); Weaknesses (Слабости); Opportunities (Возможности); Threats (Угрозы). SWOT-анализ позволяет выявить, структурировать сильные и слабые стороны компании, а также потенциальные возможности и угрозы. Достигается это за счет сравнения внутренних сил и слабостей своей компании с возможностями, которые дает им рынок. Исходя из качества соответствия, делается вывод о том, в каком направлении организация должна развивать свой бизнес, и в конечном итоге определяется распределение ресурсов по сегментам.
Цель SWOT-анализа – сформулировать основные направления развития предприятия через систематизацию имеющейся информации о сильных и слабых сторонах фирмы, а также о потенциальных возможностях и угрозах.
Самое привлекательное, в этом методе то, что информационное поле формируется непосредственно самими руководителями, а также наиболее компетентными сотрудниками компании на основании обобщения и согласования собственного опыта и видения ситуации. Общий вид матрицы первичного SWOT-анализа приведен на Рис.1.
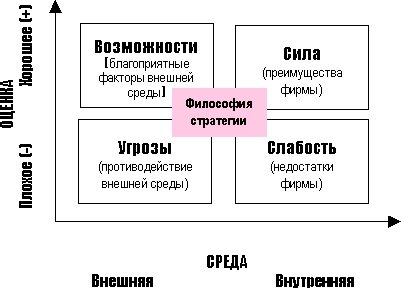
Рис.1. Матрица первичного стратегического SWOT — анализа.
На основании последовательного рассмотрения факторов, принимаются решения по корректировке целей и стратегий предприятия (корпоративных, продуктовых, ресурсных, функциональных, управленческих), которые, в свою очередь, определяют ключевые моменты организации деятельности.
Анализ бизнес-портфеля компании должен помочь менеджерам оценить поле деятельности компании. Компания должна стремиться вкладывать средства в более прибыльные области своей деятельности и сокращать убыточные. Первым шагом руководящего звена при анализе бизнес-портфеля является выявление ключевых направлений деятельности, определяющих миссию компании. Их можно назвать стратегическими элементами бизнеса – СЭБ.
На следующем этапе анализа бизнес-портфеля руководство должно оценить привлекательность различных СЭБ и решить, какой поддержки заслуживает каждое из них. В некоторых компаниях это происходит неформально в процессе работы. Руководство изучает совокупность направлений деятельности и товаров компании и, руководствуясь здравым смыслом, решает, сколько каждый СЭБ должен приносить и получать. Другие компании используют формальные методы для планирования портфеля.
Формальные методы можно назвать более точными и основательными. Среди наиболее известных и удачных методов анализа бизнес-портфеля с помощью формальных методов можно назвать следующие:
Метод BCG основан на принципе анализа матрицы рост/доля рынка. Этот метод планирования портфеля, который оценивает СЭБ компании с точки зрения темпов роста их рынка и относительной доли этих элементов на рынке. СЭБ делятся на «звезд», «дойных коров», «темных лошадок» и «собак» (см. рис. 2).
Рис.2. Матрица BCG.
Вертикальная ось на рис.2, темпы роста рынка, определяет меру привлекательности рынка. Горизонтальная ось, относительная доля рынка, определяет прочность положения компании на рынке. При делении матрицы рост/доля рынка на секторы можно выделить четыре типа СЭБ.
«Звезды». Быстро развивающиеся направления деятельности, товары, имеющие большую долю рынка. Они требуют обычно мощного инвестирования для поддержания своего роста. Со временем их рост замедляется, и они превращаются в «дойных коров».
«Дойные коровы». Направления деятельности или товары с низкими темпами роста и большой долей рынка. Этим устойчивым преуспевающим СЭБ для удержания их доли рынка требуется меньше инвестиций. При этом они приносят высокий доход, который компания использует для оплаты своих счетов и для поддержания других СЭБ, требующих инвестирования.
«Темные лошадки». Элементы бизнеса, имеющие небольшую долю быстрорастущих рынков. Они требуют большого количества средств даже для поддержания своей доли рынка, не говоря уже об ее увеличении. Руководству следует тщательно продумать, каких «темных лошадок» стоит превратить в «звезды», а какие поэтапно ликвидировать.
«Собаки». Направления деятельности и товары с низкой скоростью роста и небольшой долей рынка. Они могут приносить достаточный доход для поддержания самих себя, но не обещают стать более серьезными источниками дохода.
Каждый СЭБ выносится на данную матрицу пропорционально ее доли в валовом доходе компании. После классификации СЭБ компания должна определить роль каждого элемента в будущем. В отношении каждого СЭБ можно применить одну из четырех стратегий. Компания может увеличить инвестиции в какой-либо элемент бизнеса, чтобы отвоевать для него долю рынка. Либо она может инвестировать ровно столько, сколько нужно для сохранения доли СЭБ на текущем уровне. Она может выкачивать ресурсы из СЭБ, изымая его краткосрочные денежные ресурсы в течение определенного промежутка времени, не считаясь с отдаленными последствиями. Наконец, она может изъять капиталовложения из СЭБ, продав его или приступив к поэтапной ликвидации, и использовать ресурсы в другом месте.
С течением времени СЭБ меняет свое положение в матрице рост/доля рынка. У каждого СЭБ свой жизненный цикл. Многие СЭБ начинают как «темные лошадки» и при благоприятно складывающихся обстоятельствах переходят в категорию «звезд». Позже, по мере замедления роста рынка, они становятся «дойными коровами» и, наконец, на закате своего жизненного цикла угасают или превращаются в «собак». Компании необходимо непрерывно вводить новые товары и виды деятельности, чтобы часть из них становилась «звездами», а затем и «дойными коровами», помогающими финансировать другие СЭБ.
Матричные методы играют очень важную роль в стратегическом анализе, планировании и маркетинге. Матричный метод очень удобен – именно этим объясняется его распространенность. Однако использование только матричных методов не является достаточным, так как матрицы позволяют исследовать стратегическое планирование и маркетинг с отдельных сторон, и не показывают полной картины, но в соединении с остальными методами матричный подход дает возможность наглядно увидеть закономерности в процессах, происходящих на предприятии, и сделать правильные выводы.
Таблица 1. Матричный инструментарий в анализе и планировании деятельности организации
Методические рекомендации по МАИ
В методических указаниях представлены краткий материал по описанию метода анализа иерархий, примеры решения экономических задач, задания для самостоятельного выполнения и контрольные задания по тематике лабораторного практикума. Для магистрантов 2 курса, обучающихся по направлению 03.04.01 «Экономика» магистерской программы «Учет, анализ и аудит» (заочная форма обучения).
При системном исследовании (анализе) сложных социально-экономических систем в их развитии, как известно [6], базовая методика системного анализа включает в себя10 основных этапов:
формулировка проблемы;
формулировка проблематики;
конфигурирование проблемы;
постановка задачи;
определение глобальной цели и построение дерева целей;
выбор критериев для сравнения альтернативных путей достижения цели (далее кратко «альтернатив»);
генерирование альтернатив;
моделирование;
синтез решения;
реализация решения.
При этом предпоследний 9-й этап неизбежно связан с многокритериальным выбором оптимальной альтернативы среди нескольких, прогенерированных на седьмом этапе.
При принятии управленческих решений и прогнозировании возможных результатов лицо, принимающее решение (ЛПР), обычно сталкивается со сложной системой взаимозависимых компонент (ресурсы, желаемые исходы, цели, лица и группы лиц и т.д.), которую нужно проанализировать. Чем лучше ЛПР вникает в эту сложность, тем лучше будут его прогнозы и принимаемые решения. И в этом процессе исследования сложной системы большое значение имеет модель поддержки принятия решения ЛПР.
Если удалось связать критерии с альтернативами и ограничениями в соответствующей количественной модели исследуемой системы, то можно применить один из методов многокритериальной оптимизации [2, 8]. Однако для сложных нелинейных многомерных систем часто не удается их формализовать и описать комплексом количественных моделей. В таких случаях при решении задач многокритериального выбора прибегают к методам экспертных оценок при разработке критериев и определении наилучшей альтернативы.
Здесь возникает принципиальное затруднение, связанное с субъективным характером экспертных оценок: они сильно зависят от квалификации каждого члена группы экспертов, суждения разных экспертов могут быть плохо согласованными и алгоритм выбора оптимальной альтернативы плохо формализуем.
Рассматриваемый ниже метод анализа иерархий (МАИ), разработанный американским ученым Томасов Саати в 1968 году, во многом лишен указанных выше недостатков. В МАИ процесс разработки управленческих решений в основном формализован: экспертные оценки используются только на стадии постановки задачи при формировании так называемой «матрицы суждений». Применение метода сводит исследование даже очень сложных систем к последовательности попарных сравнений соответствующим образом определенных компонент.
Отметим основные преимущества МАИ:
Теория МАИ отражает естественный ход человеческого мышления. При анализе сложной системы для выработки управленческих решений человеческий разум объединяет их в группы в соответствии с распределением некоторых свойств между элементами. Общие свойства этих групп рассматриваются в качестве элементов следующего (снизу-вверх) уровня иерархии. Эти элементы вышестоящего уровня, в свою очередь, могут быть сгруппированы в соответствии с другим набором свойств, создавая элементы еще одного, более высокого уровня. Итак, до тех пор, пока не будет достигнут единственный элемент – вершина иерархии, который отождествляется с целью процесса принятия решения.
В МАИ сочетаются методы количественных и экспертных оценок на основе построения иерархических отношений между альтернативными объектами и критериями, а также использование рассуждений в терминах шкалы отношений. Этот метод позволяет изучать и анализировать отношения между альтернативными объектами на основе интерпретации целей отбора. В данном методе опыт и интуиция играют не менее важную роль, чем расчеты количественных показателей. Может оказаться так, что некоторый фактор с невысокой степенью влияния на величину критерия, будет обладать существенным системным влиянием из-за косвенных взаимодействий с другими важными факторами. Именно многокритериальная логика является тем методом, который позволяет рассмотреть проблему целиком и является полезным и незаменимым инструментом отбора альтернатив по множеству критериев.
МАИ сочетает в себе простоту и прозрачную логику алгоритма с общностью в аспекте возможности применения для самых разных систем.
Метод хорошо обоснован математически его автором Т. Саати в [1], а также опытом его применения автором и его последователями. Так в [1] приводится пример решения ряда серьезных задач: анализ влияния состояния «ни мир, ни война» на экономической, политической и военный статус Египта летом 1972г.; исследование транспортной системы Судана в 1973г.; анализ терроризма для агентства по контролю над вооружениями в Вашингтоне (США); решение вопроса о размещении ресурсов в соответствии с приоритетами для крупных частных, правительственных и международных концернов и др.
В настоящее время МАИ нашел свое широкое применение в задачах многокритериального принятия решений, стратегического планирования и распределения ресурсов, задачах разрешения конфликтов и других проблемах системных исследований сложных социально-экономических систем, в учебных и научных учреждениях, властных структурах и промышленных корпорациях.
Целью лабораторной работы является развитие у студентов навыков постановки и решения многокритериальных задач выбора, возникающих при решении сложных проблем в социально-экономических системах.
- еще 5 страниц замечательного текста
https://studfile.net/preview/3348062/
Прежде, чем изложить подробно алгоритм МАИ и описать пример его применения, приведем элементарные сведения о понятиях «собственный вектор» (СВ) матрицы и ее «собственное значение» (СЗ), поскольку МАИ основан на использовании этих понятий и математическим аппарате линейной алгебры.
Определение. Число λ называется собственным значением (или
характеристическим числом) квадратной матрицы А порядка n, если
можно подобрать такой n-мерный ненулевой вектор ![]() ,
что выполняется уравнение [10, с. 70]:
,
что выполняется уравнение [10, с. 70]:
![]() или
или ![]() .
(1)
.
(1)
Множество всех собственных значений ![]() матрицы
А находится как корни характеристического или «векового» уравнения
матрицы
А находится как корни характеристического или «векового» уравнения
![]() ,
(2)
,
(2)
где λ – рассматривается в качестве независимых переменных; Е – матричная единица; det(·) – определитель матрицы.
Замечание 1. Если выполнить операцию вычисления определителя det(·) в (2), то получим выражение для характеристического полинома относительно собственных чисел:
![]() .
(3)
.
(3)
Решение систем линейных однородных уравнений вида (1) и (2) основано на известной лемме из теории матриц [9, с. 54]: «Для того, чтобы линейная система однородных алгебраических уравнений имела нетривиальное решение, необходимо и достаточно равенство нулю ее определителя».
Пример. Найти собственные значения и собственные векторы матрицы
![]() .
.
Запишем характеристическое уравнение матрицы
![]() .
.
То есть получилось квадратное уравнение (характеристический многочлен) относительно неизвестных значений λ.
Решением этого квадратного уравнения будут корни:
![]() .
.
Найдем собственные векторы, принадлежащие собственным
значениям. Собственный вектор, принадлежащий собственному значению ![]() ,
по определению является ненулевым решением системы
,
по определению является ненулевым решением системы
![]() .
(4)
.
(4)
Верхний индекс в скобках означает принадлежность к собственному значению ![]() ,
а нижний индекс – это номер простого (не кратного) корня.
,
а нижний индекс – это номер простого (не кратного) корня.
Поучим:
 .
.
Проверяем условие цитированной выше леммы:
![]() .
.
Условия выполнены, значит нетривиальное решение (3) существует. Тогда в простейшем случае системы двух уравнений [9, с. 336]:

Таким образом, ненулевой собственный вектор, принадлежащий собственному числу ![]() ,
найден:
,
найден:
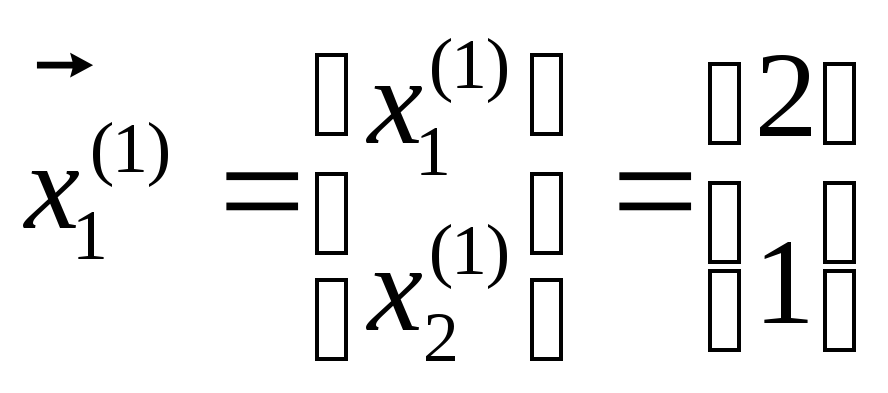 .
.
Аналогично находится второй собственный вектор ![]() матрицыА,
принадлежащий собственному значению
матрицыА,
принадлежащий собственному значению ![]() .
.
 ;
; ![]()

Следовательно, второй собственный вектор, принадлежащий собственному числу ![]() ,
равен
,
равен
![]() .
.
Замечание. Метод нахождения собственных чисел ![]() и
собственных векторов из [9, с. 336] неэффективен с точки зрения вычислительной
математики при высоком порядке матрицыА (n ~ сотни и тысячи).
и
собственных векторов из [9, с. 336] неэффективен с точки зрения вычислительной
математики при высоком порядке матрицыА (n ~ сотни и тысячи).
В вычислительной математике известны различные вычислительные схемы определения собственных чисел и собственных векторов матрицы, и имеются соответствующие пакеты программ для ЭВМ. Однако до настоящего времени общепринятый стандартный простой метод решения проблемы на собственные значения и собственные векторы матриц большого размера отсутствует.
Если под рукой нет подходящей программы, то можно применить один из простых приближенных методов, описанных в [1, с. 32]. В лабораторной работе применен метод под номером 4, использующий среднегеометрическую оценку компонент собственного вектора (см. ниже таблицу 6).
Программа для МАИ методом СААТИ за 50 руб на год
https://fox-smile.ru/analiz-ierarhij-metodom-saati/
https://helpdiss.ru/shop/programma-analiza-ierarhij-mai-metodom-t-saati/
https://helpdiss.ru/programma-analiza-ierarhij-metodom-t-saati/?
|
|

